计算流体力学和流固耦合算法

北京理工大学 | 李明健

计算流体力学（Computational Fluid Dynamics，CFD）是数学、流体力学和计算机的交叉学科，主要通过数值方法求对流体力学问题进行模拟和分析；流固耦合（Fluid-Structural Interaction，FSI）是流体和固体相互影响、相互作用的问题，是流体力学和固体力学的交叉领域。计算流体力学算法和流固耦合算法在航空、航天、能源、国防、海洋、交通等领域均具有重要的研究意义，在其基础上建立的仿真工具和软件，是数值模拟的国之重器。团队面向不可压缩流体、可压缩流体、多相流动问题、流固耦合问题的数值模拟开展研究，旨在推动计算力学新理论与新算法发展，为我国自主CAE软件和战略软装备的发展贡献力量。

该研究方向代表性成果如下：

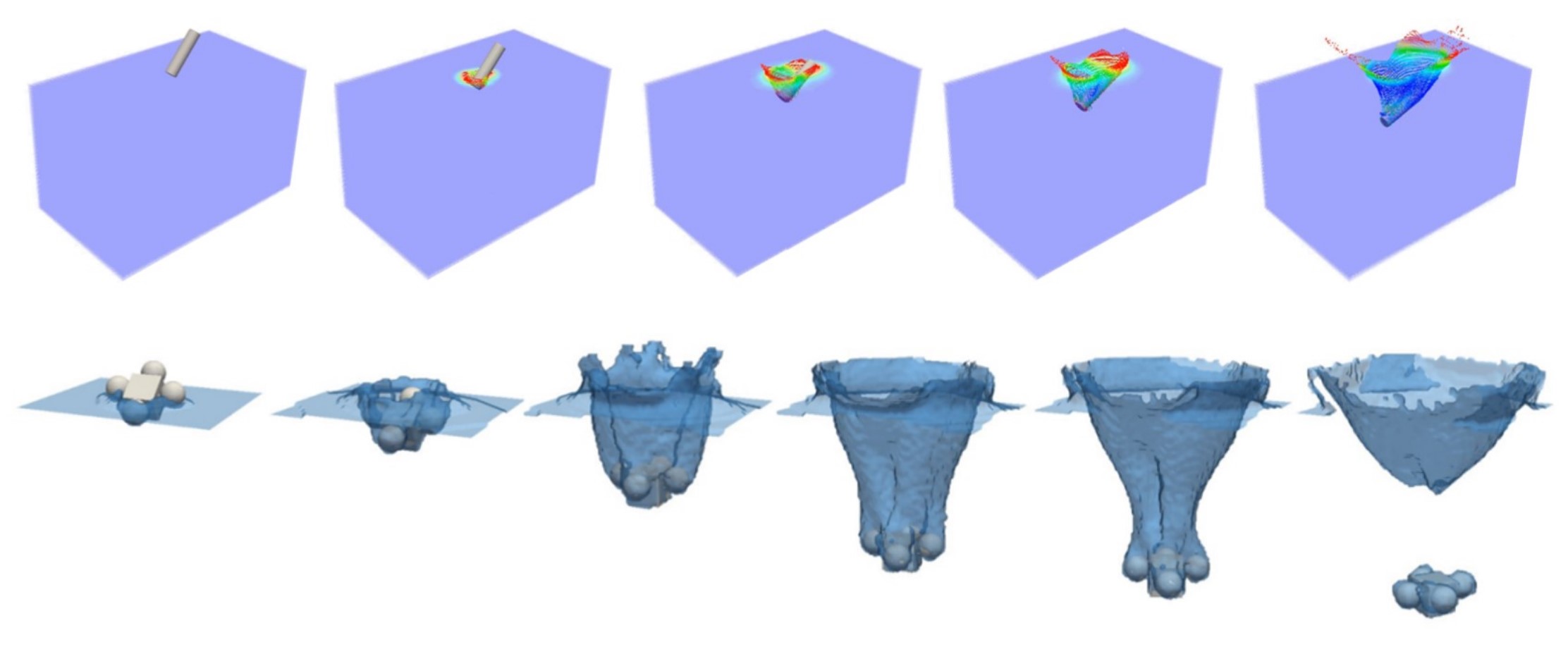
不可压浸入物质点有限元法（CMAME）：面向入水问题，通过示踪点、网格标记和粒子重整技术和分区耦合的方式，实现了对气-液-固三相界面的快速追踪，以及考虑结构大变形和自由液面演化的流固耦合问题求解。

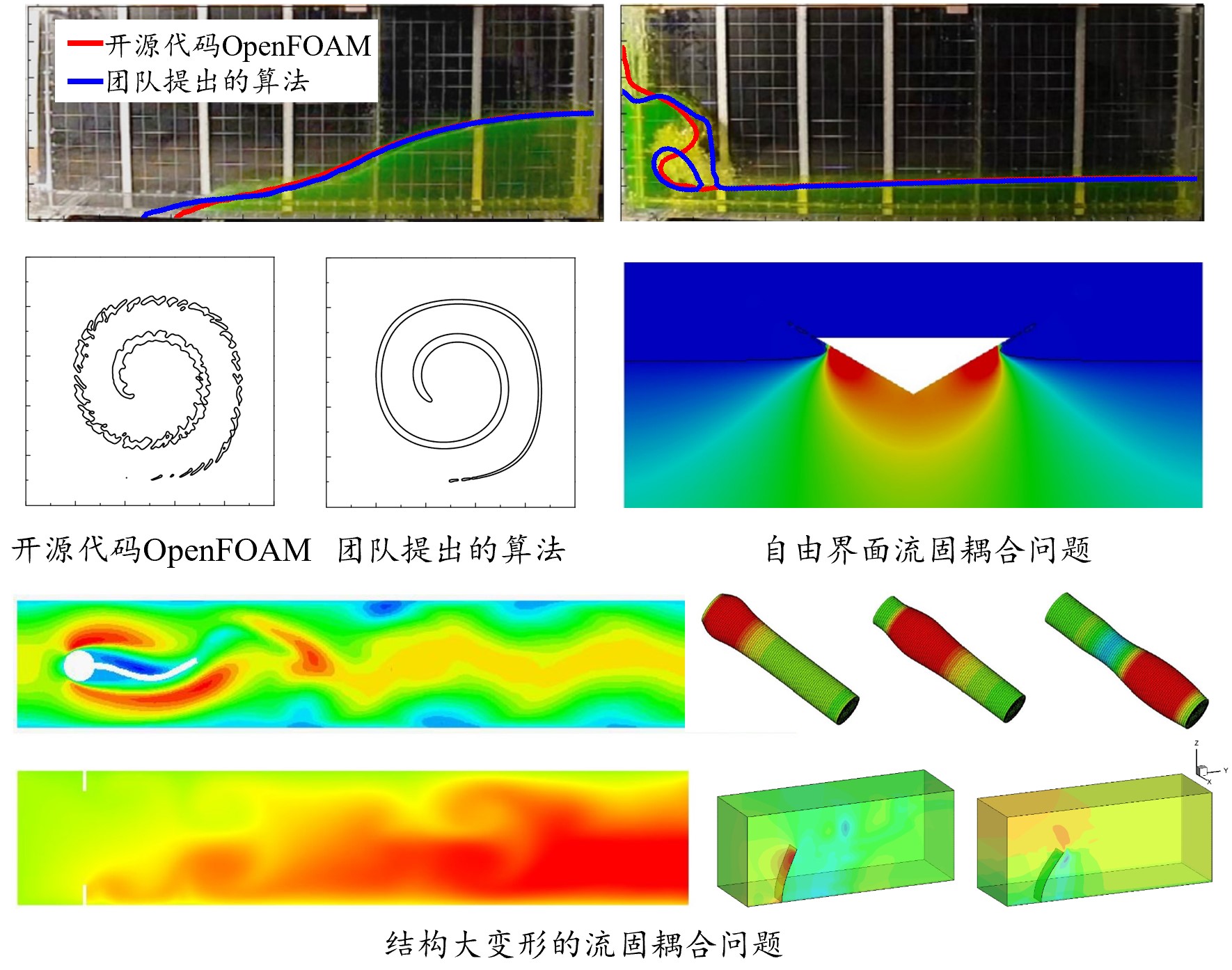
有限体积法/任意拉格朗日-欧拉方法（CAMWA，CAS，ATE，以及未发表结果）：面向不可压流体力学问题和流固耦合问题，发展了基于任意拉格朗日-欧拉（ALE）描述的有限体积-有限元耦合方法、基于二阶界面重构流体体积法（VOF）和ALE描述的流固耦合方法、基于相容守恒格式和网格扩散变形技术的磁-热-流-固耦合方法等，实现了对流固耦合中自由液面的高精度捕捉、以及考虑结构大变形的流固耦合高精度求解。

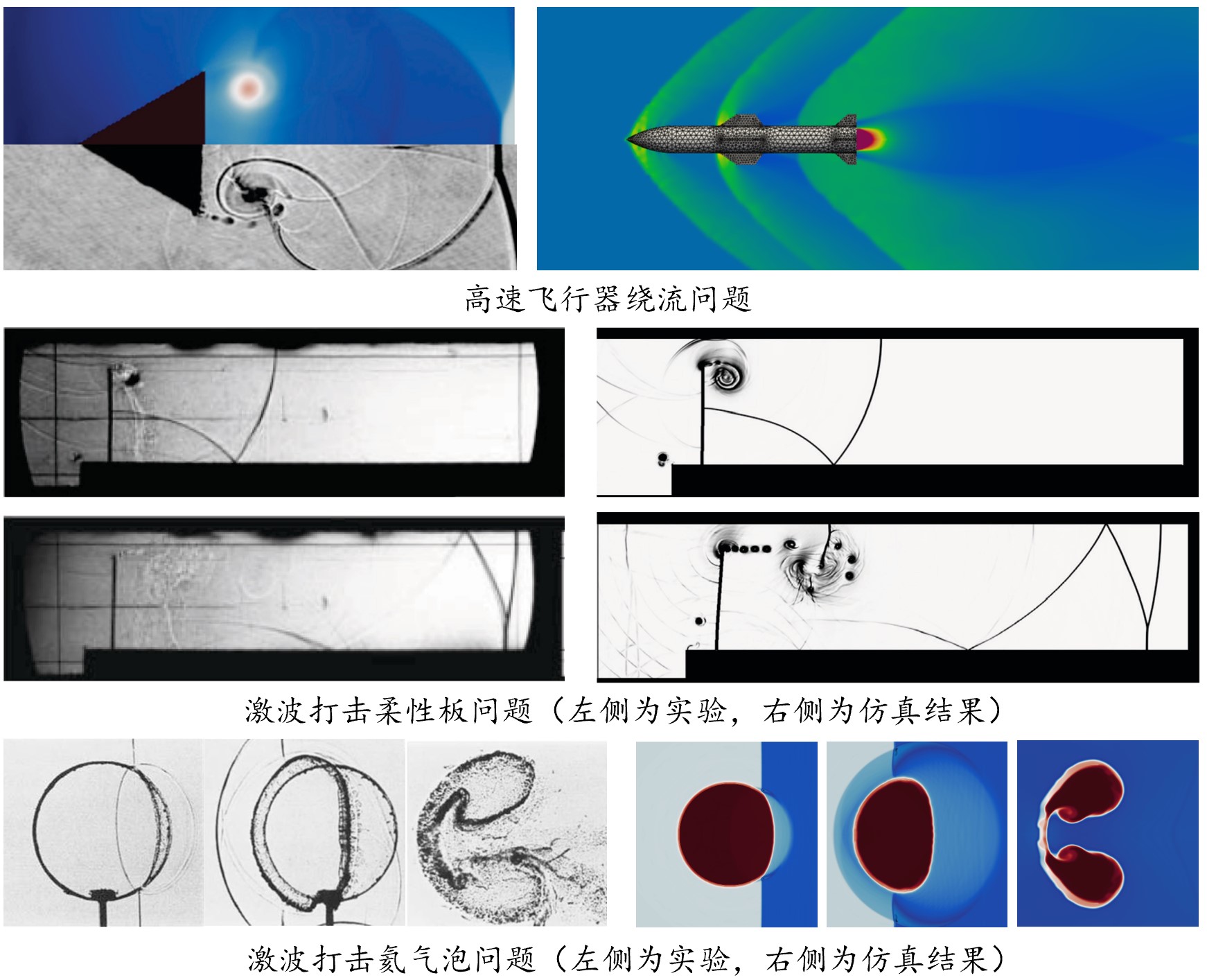
有限差分法/浸入边界法（未发表结果）：面向高超音速流动、爆炸等可压缩流体力学问题和流固耦合问题，发展了基于高精度WENO格式有限差分法、水平集法（Levelset）、虚拟流体法（GFM）和浸入边界法（IBM）的流固耦合算法，实现了对高速飞行器气动力学问题、爆炸驱动流固耦合问题、激波捕捉、多介质流动问题的高精度求解。