Vibration of a mass-spring-damper system

Beijing Institute of Technology | Ming-Jian Li

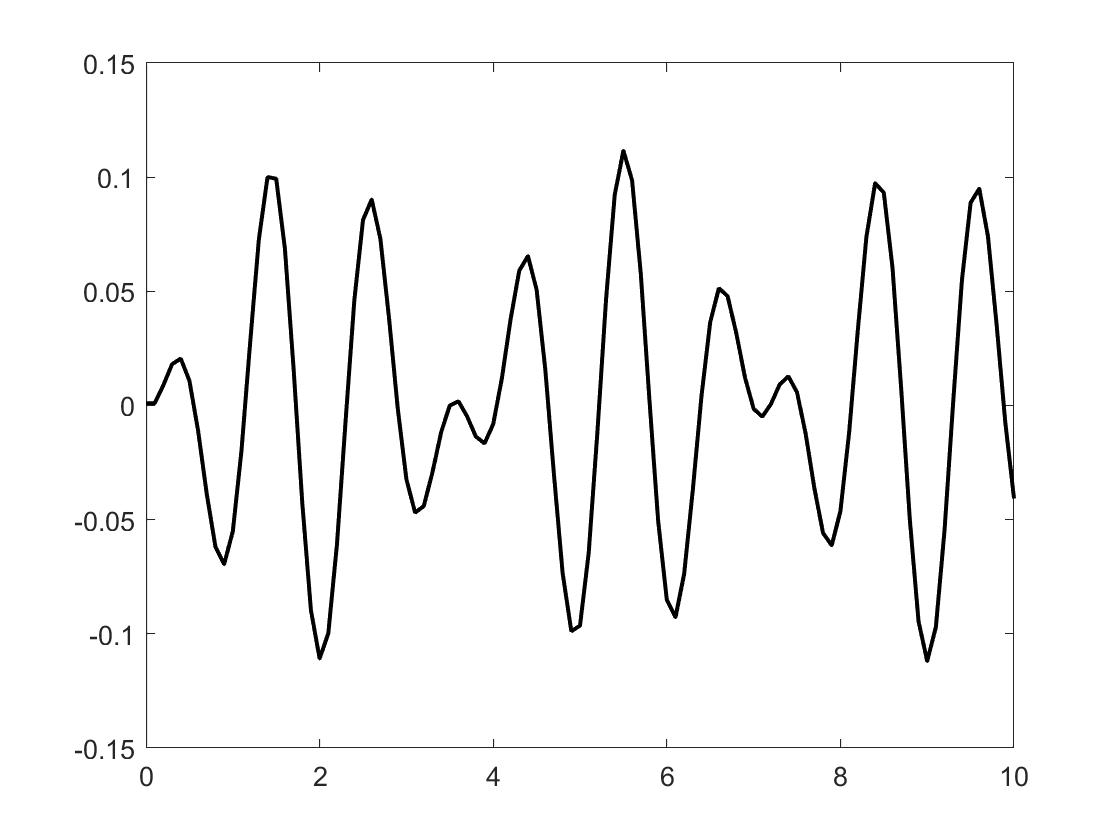
The following MATLAB code is a companion code for the course on Artificial Intelligence and Simulation Science. It functions to calculate the vibration of a mass point under the action of spring force, external excitation, and damping, with time integration performed using the forward Euler method.

1
clear; clc;
2
m=0.1;
3
k=2; 
4
% forced vibration
5
Fmag=0.1;  
6
% natrual = sqrt(k/m)/2/pi 
7
% 0.7118 will cause resonance
8
freq=1;  
9
omg=freq*2*pi;
10
% damp
11
c=0;
12
% time
13
dt = 0.1;  
14
tend = 10;
15
t_ = 0 : dt : tend;
16
d = zeros(length(t_), 1);
17
d(2) = 0.001;
18
a=k*d(2);
19
d(1) = d(2)+dt^2/2*a;
20
for n = 2 : length(t_)-1
21
    t = t_(n);
22
    F = Fmag*cos(omg*t);
23
    rhs = F - (k-2/dt^2*m)*d(n) - (m/dt^2-c/2/dt)*d(n-1);
24
    coef = m/dt^2 + c/2/dt;
25
    d(n+1) = rhs/coef;
26
    clf
27
    plot(t_, d, 'k', "LineWidth", 1.5)
28
    hold on
29
    pause(0.01);
30
end

The result is as follows. With different input parameters, the vibration differs a lot.