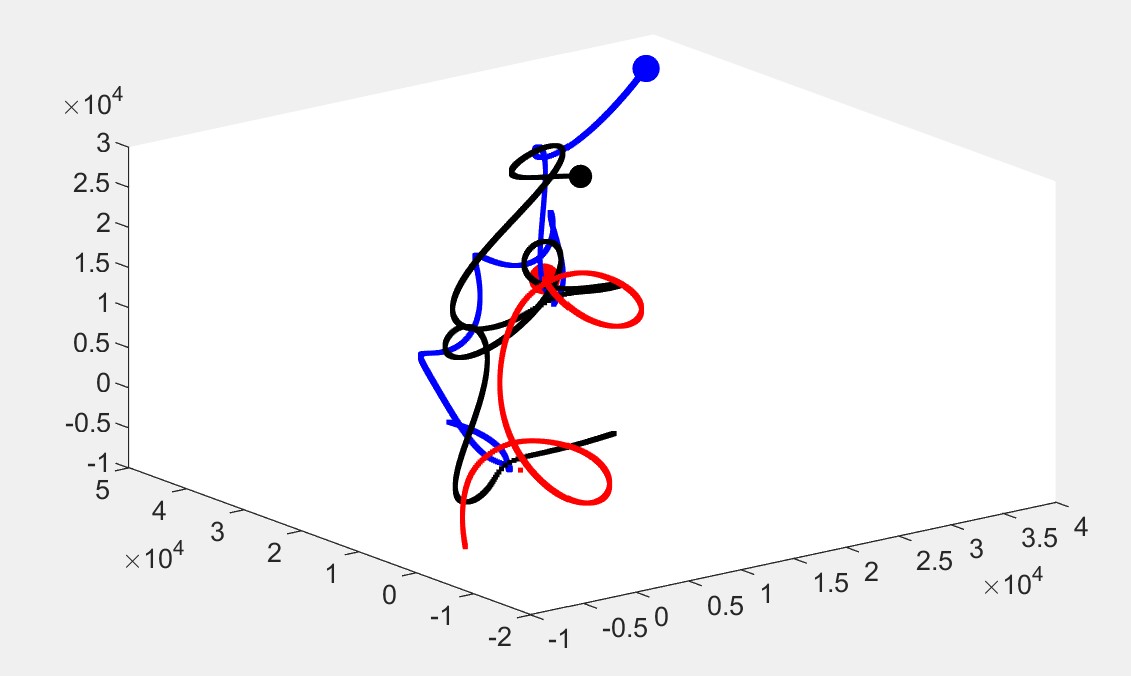
Simulation of the three-body problem

Beijing Institute of Technology | Ming-Jian Li

The following MATLAB code is a companion code for the course on Artificial Intelligence and Simulation Science. It functions to calculate the trajectories of three celestial bodies under the influence of mutual gravity, with time integration performed using the forward Euler method.

49
1
clear; clc;
2

3
m1 = 5e4;
4
m2 = 4e4;
5
m3 = 3e4;
6

7
v1 = [2 5 3];
8
v2 = [2 -3 -1];
9
v3 = [-1.5 1.5 -0.9];
10

11
G= 10;
12

13
dt = 15;
14
tend = 60000;
15
t = 0 : dt : tend;
16

17
p1 = zeros(length(t), 3);
18
p2 = zeros(length(t), 3);
19
p3 = zeros(length(t), 3);
20

21
p1(1,:)=[-8000 -5000 -6000];
22
p2(1,:)=[-3000 7000 5000];
23
p3(1,:)=[5000 -7000 5000];
24

25
set(gcf,'Position',[200 200 1080 720]); 
26

27
for i = 2 : length(t)
28
    x1 = p1(i-1,:);
29
    x2 = p2(i-1,:);
30
    x3 = p3(i-1,:);
31
    a1 = G*m2 * (x2-x1) / norm(x2-x1).^3 + G*m3*(x3-x1) / norm(x3-x1).^3;
32
    a2 = G*m3 * (x3-x2) / norm(x3-x2).^3 + G*m1*(x1-x2) / norm(x1-x2).^3;
33
    a3 = G*m1 * (x1-x3) / norm(x1-x3).^3 + G*m2*(x2-x3) / norm(x2-x3).^3;
34
    v1 = v1 + a1 * dt;
35
    v2 = v2 + a2 * dt;
36
    v3 = v3 + a3 * dt;
37
    p1(i,:) = p1(i-1,:) + v1 * dt;
38
    p2(i,:) = p2(i-1,:) + v2 * dt;
39
    p3(i,:) = p3(i-1,:) + v3 * dt; 
40
    clf
41
    plot3(p1(i,1), p1(i,2), p1(i,3), 'r.', "MarkerSize", 40)
42
    hold on
43
    plot3(p2(i,1), p2(i,2), p2(i,3), 'b.', "MarkerSize", 35)
44
    plot3(p3(i,1), p3(i,2), p3(i,3), 'k.', "MarkerSize", 30)
45
    plot3(p1(:,1), p1(:,2), p1(:,3), 'r.', "LineWidth", 1.5)
46
    plot3(p2(:,1), p2(:,2), p2(:,3), 'b.', "LineWidth", 1.5)
47
    plot3(p3(:,1), p3(:,2), p3(:,3), 'k.', "LineWidth", 1.5)
48
    pause(0.001);
49
end

The results are as follows.