弹性力学平衡方程的推导

北京理工大学 | 李明健

我们假设在弹性体中，有一个微元六面体，它的长宽高分别为 ， ， ，微元体在 面上的正应力和剪应力为：

根据泰勒公式，函数 在 处展开为：

则应力在 处泰勒展开为：

略去高阶项，得到：

同理可以得到其他应力形式，最终微元体上的受力如下图：

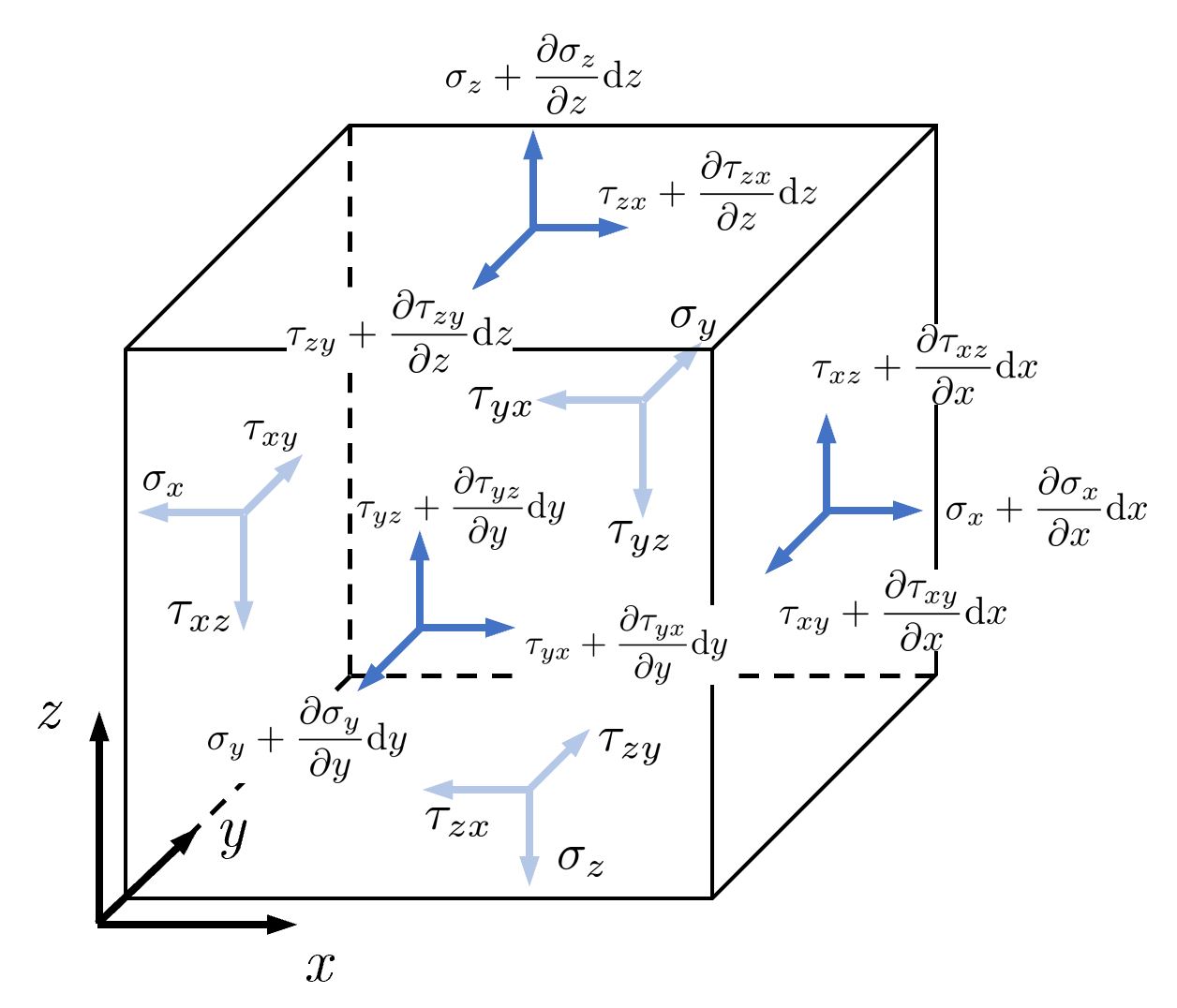
剪应力互等原理：

我们取平行于 轴的一条直接，分别过微元体左右两个面的中点，以这条直线为转轴，根据力矩和为零，得到：

整理得到：

略去小量，得到：

同理得到：

这就是剪应力互等原理。

平衡微分方程：

以 方向为例，面上的正应力和剪应力和应该等于体积上的体力，即：

其他两个方向同理，三个方程整理，即得到静力学平衡微分方程：

或写作：

对于动力学问题，则加上惯性力和阻尼力，形式如下：

以上。