三维八节点六面体单元的单元刚度矩阵推导

北京理工大学 | 李明健

对于三维八节点六面体单元，采用如下的节点编号规则：

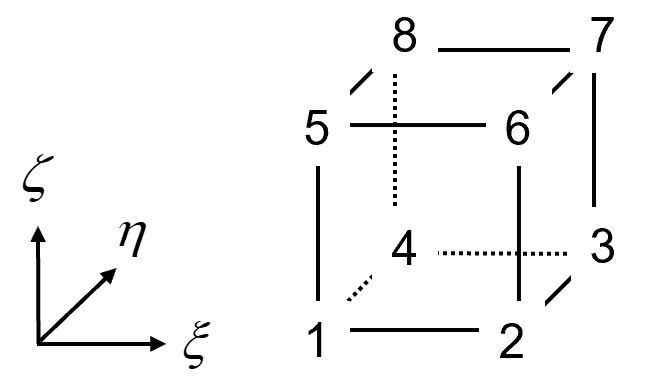
我们知道单元刚度矩阵为：

k=∫ΩBTDBdΩ

其中 B 为单元应变矩阵：

B=[∂N1∂x00...∂N8∂x000∂N1∂y0...0∂N8∂y000∂N1∂z...00∂N8∂z∂N1∂y∂N1∂x0...∂N8∂y∂N8∂x00∂N1∂z∂N1∂y...0∂N8∂z∂N8∂y∂N1∂z0∂N1∂x...∂N8∂z0∂N8∂x]6×24

各节点的形函数写为局部坐标的形式：

Ni=18(1+ξiξ)(1+ηiη)(1+ζiζ)

D 为弹性矩阵：

D=[λ+2Gλλ000λλ+2Gλ000λλλ+2G000000G000000G000000G]6×6

拉梅系数 λ 和 G 为：

λ=Eμ(1+μ)(1−2μ),G=E2(1+μ)

这样，单刚 k 就是一个 24×24 的矩阵。

为了得到单刚的具体形式，需要将全局坐标转化为局部坐标：

k=∭ΩBTDBdxdydz=∫−11∫−11∫−11BTDB|J|dξdηdζ

由于任一点处的全局坐标 x,y,z 可以写为如下形式：

x=∑i=18Nixi,y=∑i=18Niyi,z=∑i=18Nizi

因此 dxdydz 向局部坐标转化时，引入了雅克比矩阵：

J=[∂x∂ξ∂y∂ξ∂z∂ξ∂x∂η∂y∂η∂z∂η∂x∂ζ∂y∂ζ∂z∂ζ]3×3=[∑i=18∂Ni∂ξxi∑i=18∂Ni∂ξyi∑i=18∂Ni∂ξzi∑i=18∂Ni∂ηxi∑i=18∂Ni∂ηyi∑i=18∂Ni∂ηzi∑i=18∂Ni∂ζxi∑i=18∂Ni∂ζyi∑i=18∂Ni∂ζzi]3×3=[∂N1∂ξ∂N2∂ξ...∂N8∂ξ∂N1∂η∂N2∂η...∂N8∂η∂N1∂ζ∂N2∂ζ...∂N8∂ζ]3×8[x1y1z1x2y2z2⋮⋮⋮x8y8z8]8×3

其中将形函数对局部坐标的偏导数矩阵写为：

∂N∂ξ=[∂N1∂ξ∂N2∂ξ...∂N8∂ξ∂N1∂η∂N2∂η...∂N8∂η∂N1∂ζ∂N2∂ζ...∂N8∂ζ]3×8

将单元8个节点的坐标矩阵写为：

x=[x1y1z1x2y2z2⋮⋮⋮x8y8z8]8×3

则雅克比矩阵可简写为：

J=∂N∂ξx

下面我们看应变矩阵，由于 B 矩阵中 ∂Ni∂x,∂Ni∂y,∂Ni∂z 需要对全局坐标求导，可以用以下方式根据形函数局部坐标偏导得到，首先把形函数对全局坐标的偏导数写成矩阵形式：

∂N∂x=[∂N1∂x∂N2∂x...∂N8∂x∂N1∂y∂N2∂y...∂N8∂y∂N1∂z∂N2∂z...∂N8∂z]3×8

根据链式法则：

∂Ni∂ξ=∂Ni∂x∂x∂ξ+∂Ni∂y∂y∂ξ+∂Ni∂z∂z∂ξ∂Ni∂η=∂Ni∂x∂x∂η+∂Ni∂y∂y∂η+∂Ni∂z∂z∂η∂Ni∂ζ=∂Ni∂x∂x∂ζ+∂Ni∂y∂y∂ζ+∂Ni∂z∂z∂ζ

即

[∂N1∂ξ∂N2∂ξ...∂N8∂ξ∂N1∂η∂N2∂η...∂N8∂η∂N1∂ζ∂N2∂ζ...∂N8∂ζ]3×8=[∂x∂ξ∂y∂ξ∂z∂ξ∂x∂η∂y∂η∂z∂η∂x∂ζ∂y∂ζ∂z∂ζ]3×3[∂N1∂x∂N2∂x...∂N8∂x∂N1∂y∂N2∂y...∂N8∂y∂N1∂z∂N2∂z...∂N8∂z]3×8

则 B 矩阵中的全局偏导数可以用以下方式求得：

∂N∂x=J−1∂N∂ξ

即

[∂N1∂x∂N2∂x...∂N8∂x∂N1∂y∂N2∂y...∂N8∂y∂N1∂z∂N2∂z...∂N8∂z]3×8=[∂x∂ξ∂y∂ξ∂z∂ξ∂x∂η∂y∂η∂z∂η∂x∂ζ∂y∂ζ∂z∂ζ]3×3−1[∂N1∂ξ∂N2∂ξ...∂N8∂ξ∂N1∂η∂N2∂η...∂N8∂η∂N1∂ζ∂N2∂ζ...∂N8∂ζ]3×8

通过这种方式得到了 ∂Ni∂x,∂Ni∂y,∂Ni∂z ，然后对应填到 B 矩阵中，即得到应变矩阵。

为了求积分，采用数值积分方式，通常为2点高斯积分：

k=∭ΩBTDBdxdydz=∫−11∫−11∫−11BTDB|J|dξdηdζ=∑i2∑j2∑k2wiwjwkBijkTDBijk|J|ijk

其中 wi,wj,wk 为权重，2点高斯积分中均为 1，积分点坐标在三个方向分别为 -0.57735026918963, 0.57735026918963，对8个高斯积分点叠加，就得到了单元刚度矩阵。

以上。