含两相介质的温度方程求解方法

北京理工大学 | 李明健

在不可压缩两相流动问题中，通常可以采用 one-fluid 模型，即用统一的物理场描述两种流体，用体积分数的方式区分两相介质。例如，密度场可表示为如下形式：

其中 $\alpha$$\alpha$ 为体积分数，${\rho }_1$$\rho_1$ 和 ${\rho }_2$$\rho_2$ 分别为两种流体（如水、气）的密度。比热容等其他物理量用同样的方式处理。

对于含两相流动的传热问题，需要满足质量、动量、能量守恒，还需要考虑体积分数的输运。这里，我们仅关注温度方程的求解。

控制方程

温度方程的守恒形式写为如下形式：

其中 $\rho ,c,T,\lambda ,\mathit{u},Q$$\rho, c, T, \lambda, \boldsymbol u, Q$ 分别是密度、比热容、温度、热导率、速度、体积热源。

温度方程更新的离散如下：

其中 $C$$C$ 为对流项的离散形式，已经包含了时间步长 $\mathrm{\Delta }t$$\Delta t$ 的影响，$D$$D$ 为扩散项，$Q$$Q$ 为热源项。

对流项

对流项具体展开形式为：

其中 $u,v,w$$u,v,w$ 分别为 $x,y,z$$x,y,z$ 三个方向的速度分量。

在有限体积法中，根据奥-高公式，将体积分变成面积分，对流项表示如下：

对于单介质，可以采用一阶、二阶迎风格式处理对流项，对于两相介质来说，采用几何切割的方式计算通量更为准确，更能体现相界面的影响。事实上，这也是一种迎风格式，面上的通量是由上游网格贡献的。

根据已知的面心速度场 $\mathit{u}$$\boldsymbol u$，计算在时间步长 $\mathrm{\Delta }t$$\Delta t$ 内，通过单元各个面的能量通量。以图中 $x$$x$ 方向通量为例，当 $u$$u$ 在该面上向 $x$$x$ 正方向流出时，其面心上的通量需要根据上游单元确定。假设在速度驱动下，时间步 $\mathrm{\Delta }t$$\Delta t$ 内上游单元被界面分割的目标流体穿过该面的体积为 $V^x$$V^{x}$，即下图中深色部分的体积，则该面上的通量为：

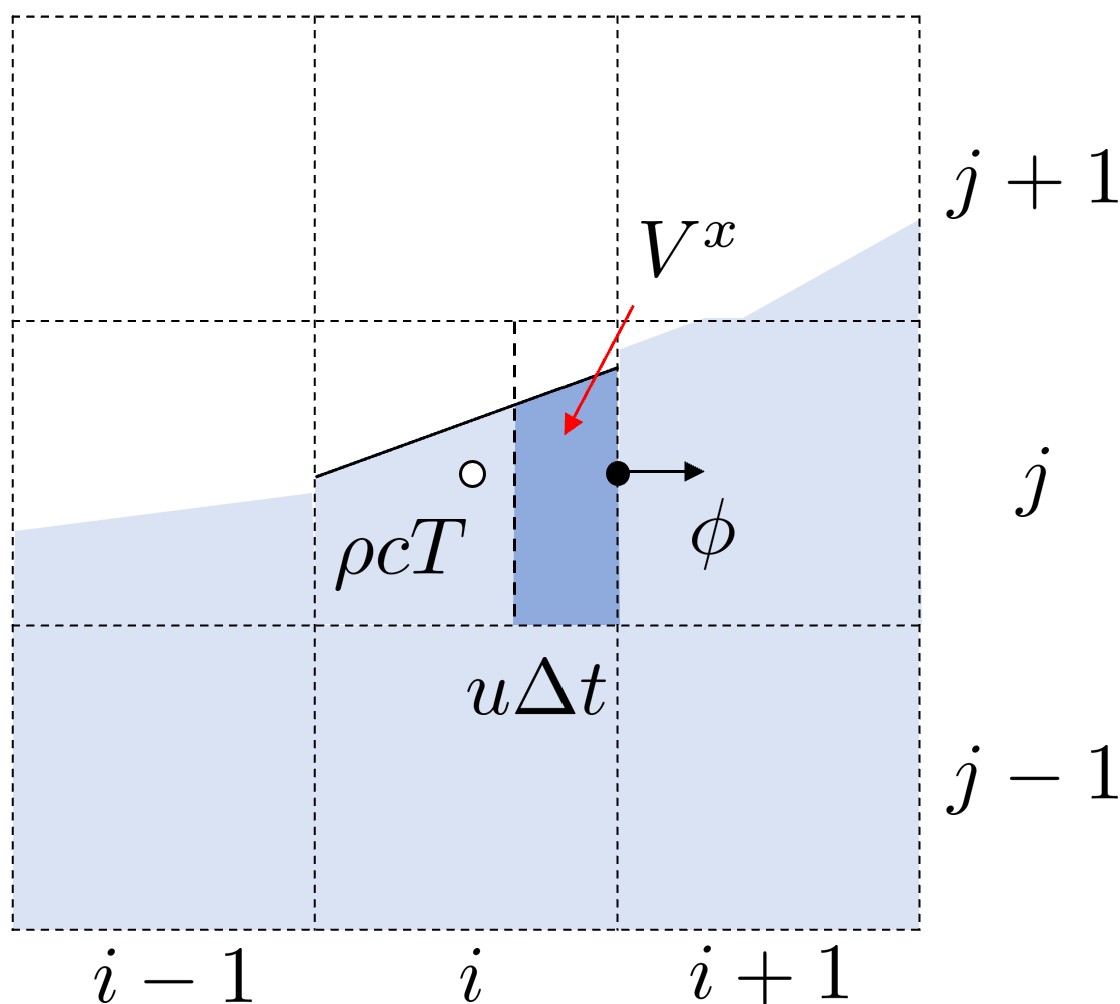
当速度为负时，通量根据下游单元确定。图中白点表示当前已知变量位置，黑点表示待求变量位置。

对流项的离散格式如下：

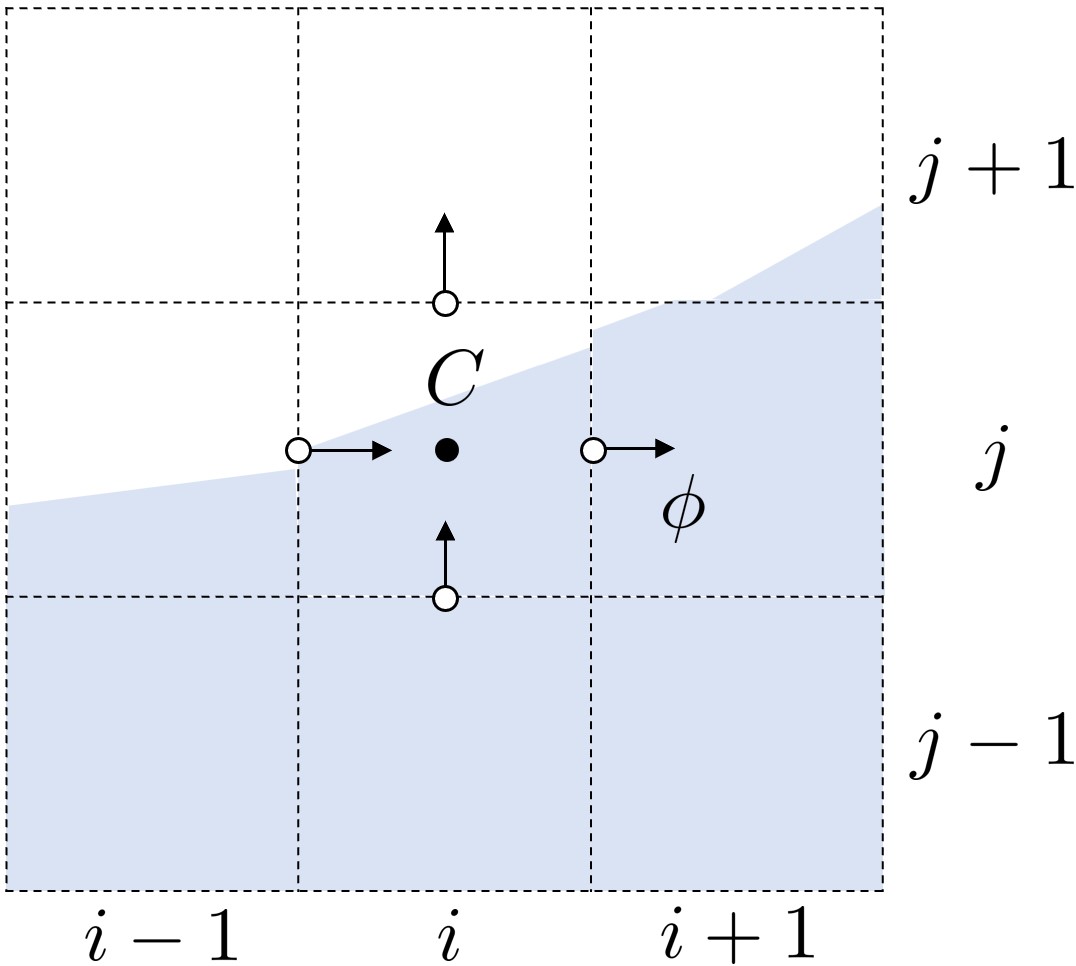
扩散项

将体积分变成面积分，扩散项表示如下：

采用二阶中心差分计算扩散项：

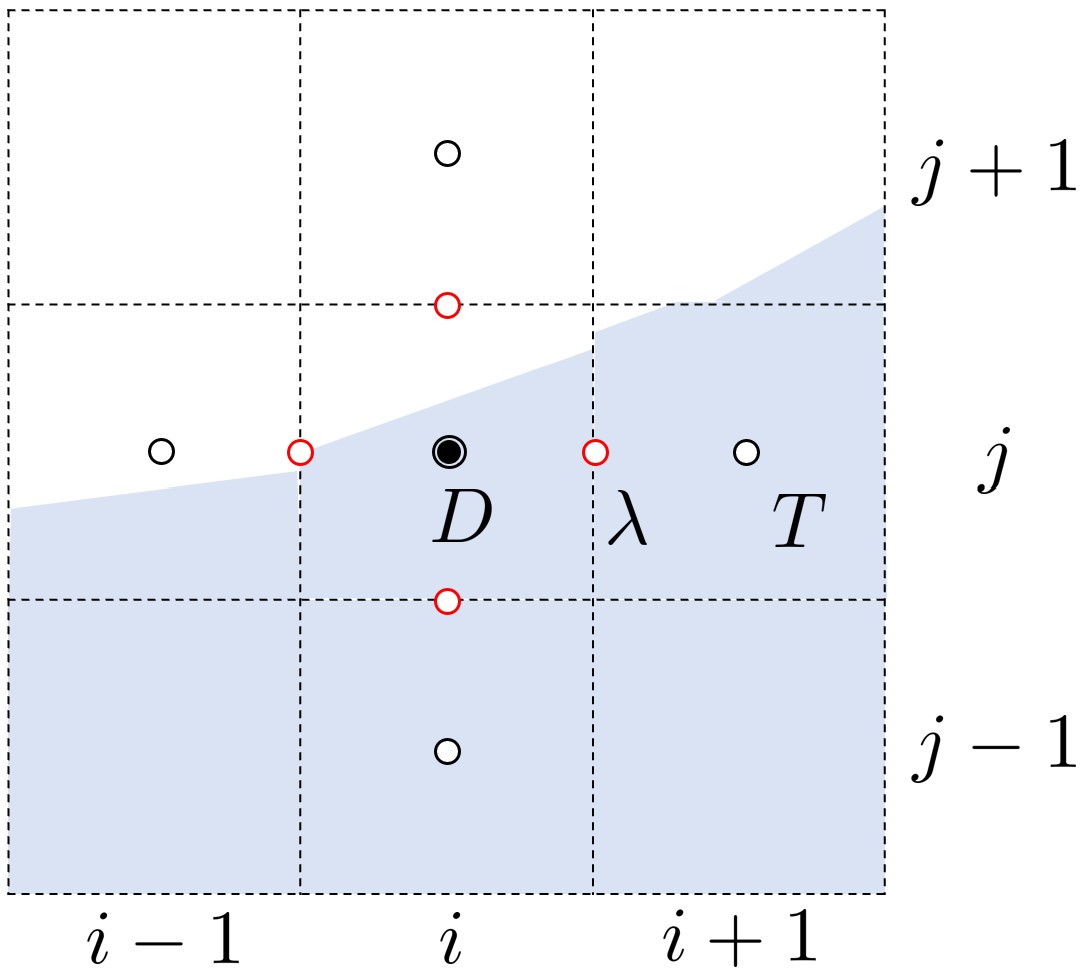
其中 $T$$T$ 需要格心值，而 $\lambda$$\lambda$ 需要面心的值。由于面心并不储存热导率，需要从格心进行插值，算术平均的精度较低，可以采用调和平均，或根据 VOF 方法中的几何切割方法，计算面上的体积分数，再根据体积分数加权计算得到面上的热导率 $\lambda$$\lambda$。