同轴厚壁圆筒共轭传热问题的解析解

北京理工大学 | 李明健

$r_1$ $r_2$ $r_2$ $r_3$ ，采用柱坐标系，假设垂直于纸面方向无限，则问题可以转化为一维热传导问题。

vof1

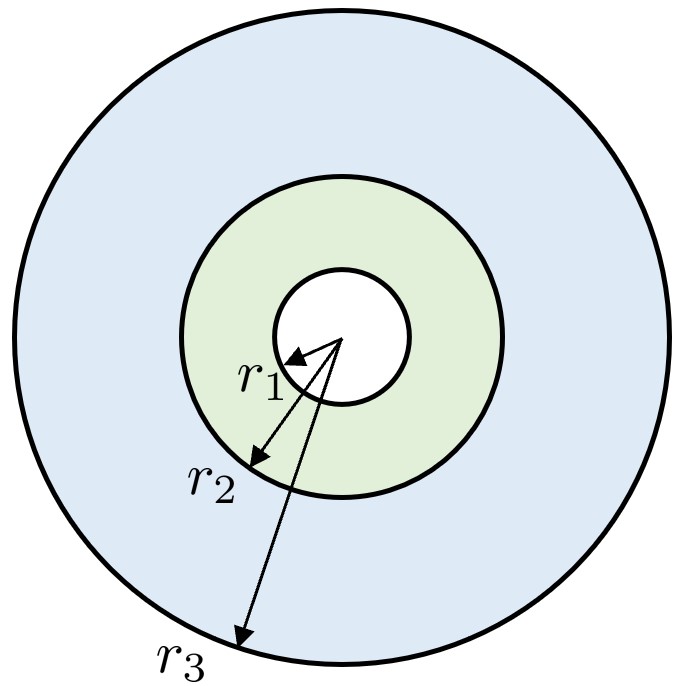
不考虑内热源，已知稳态热传导微分方程为：

\begin{matrix} (1) & - λ \nabla^{2} T = 0 \end{matrix}

$\lambda$ $\lambda_1$ $\lambda_2$ $T_1$ $T_2$ 表示，则热传导微分方程简化后可表示为：

\begin{matrix} (2) & \begin{matrix} \frac{d}{d r} (r \frac{d T_{1}}{d r}) = 0 r_{1} < r < r_{2} \\ \frac{d}{d r} (r \frac{d T_{2}}{d r}) = 0 r_{2} < r < r_{3} \end{matrix} \end{matrix}

边界条件为以下定温边界条件：

\begin{matrix} (3) & \begin{matrix} T = T^{*}, r = r_{1} \\ T = T^{* *}, r = r_{3} \end{matrix} \end{matrix}

在两个筒的界面处，应该同时满足温度连续和热流连续条件如下：

\begin{matrix} (4) & \begin{matrix} T_{1} = T_{2}, r = r_{2} \\ λ_{1} \frac{d T_{1}}{d r} = λ_{2} \frac{d T_{2}}{d r}, r = r_{2} \end{matrix} \end{matrix}

方程（2）的通解为：

\begin{matrix} (5) & T_{1} = A_{1} \ln r + B_{1}, T_{2} = A_{2} \ln r + B_{2} \end{matrix}

将以上边界条件代入，可以得到待定系数，回代后，得到温度解析解为：

\begin{matrix} (6) & \begin{matrix} T = {\begin{array}{r} T^{*} + (T^{* *} - T^{*}) \frac{\ln (\frac{r}{r_{1}})}{\ln (\frac{r_{2}}{r_{1}}) + \frac{λ_{1}}{λ_{2}} \ln (\frac{r_{3}}{r_{2}})} r_{1} < r < r_{2} \\ T^{* *} + (T^{* *} - T^{*}) \frac{\frac{λ_{1}}{λ_{2}} \ln (\frac{r}{r_{3}})}{\ln (\frac{r_{2}}{r_{1}}) + \frac{λ_{1}}{λ_{2}} \ln (\frac{r_{3}}{r_{2}})} r_{2} < r < r_{3} \end{array} \end{matrix} \end{matrix}

$T^*$ $T^{**}$ $\lambda_1$ $\lambda_2$ $r_1$ $r_2$ $r_3$ 分别为1,2,3，则该解的 matlab 代码如下：


1
clear; clc;
2
r1=1;r2=2;r3=3;
3
k1=1;k2=2;
4
T0=10;T00=100;
5
r_ = linspace(r1,r3,200);
6
for i = 1:length(r_)
7
    r=r_(i);
8
    if r>=r1 && r<=r2
9
        T(i)=T0+(T00-T0)*log(r/r1)/(log(r2/r1)+k1/k2*log(r3/r2));
10
    else
11
        T(i)=T00+(T00-T0)*k1/k2*log(r/r3)/(log(r2/r1)+k1/k2*log(r3/r2));
12
    end
13
end
14
plot(r_,T)

采用有限元方法求解该问题，ansys apdl 代码如下：


xxxxxxxxxx
50
1
finish
2
/clear
3
/prep7
4
ET,1,279
5
mp,kxx,1,1
6
mp,kxx,2,2  
7
r1=1
8
r2=2
9
r3=3
10
h=1
11
T1=10
12
T2=100
13
cylind,r1,r2,0,h,0,360 
14
cylind,r2,r3,0,h,0,360 
15
vglue,all
16
numcmp,all
17
alls
18
ESIZE,0.2
19
VSEL,s,,,1,
20
mat,1
21
vsweep,all  
22
VSEL,s,,,2
23
mat,2
24
vsweep,all  
25
alls
26
csys,1
27
nsel,s,loc,x,r1
28
d,all,temp,T1 
29
nsel,s,loc,x,r3
30
d,all,temp,T2 
31
alls
32
/solu
33
solve
34
csys,0
35
/post1
36
PATH,p1,2,30,200,   
37
PPATH,1,,r1,0,0
38
PPATH,2,,r3,0,0
39
AVPRIN,0, , 
40
PDEF, p1,Temp, ,AVG  
41
PAGET,rstz,TABLE
42
*CREATE,out,mac
43
*cfopen,T,dat
44
*VWRITE,'r','T'
45
%C, %C
46
*VWRITE,rstz(1,1),rstz(1,5)
47
%G, %G
48
*cfclose
49
*END
50
/INPUT,out,mac

有限元计算结果如下：

vof1

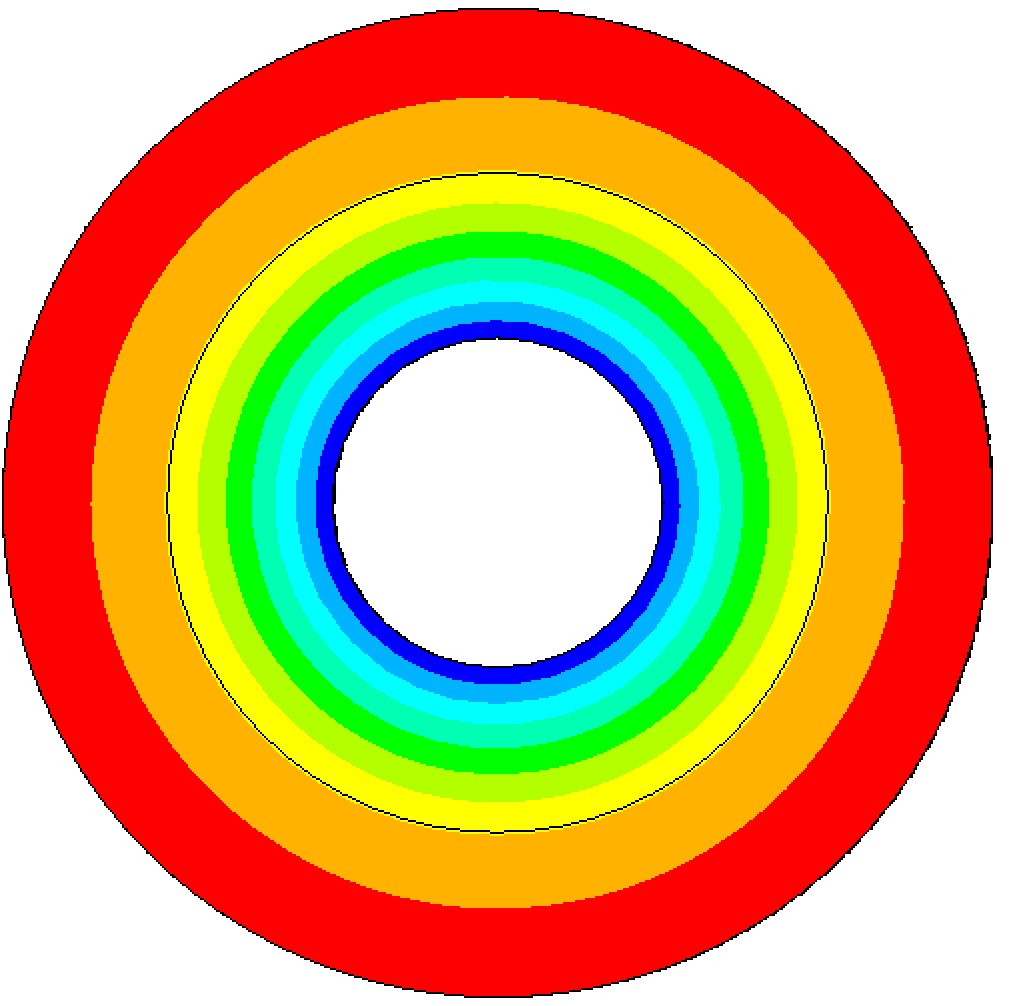
解析解和有限元结果对比如下：

vof1

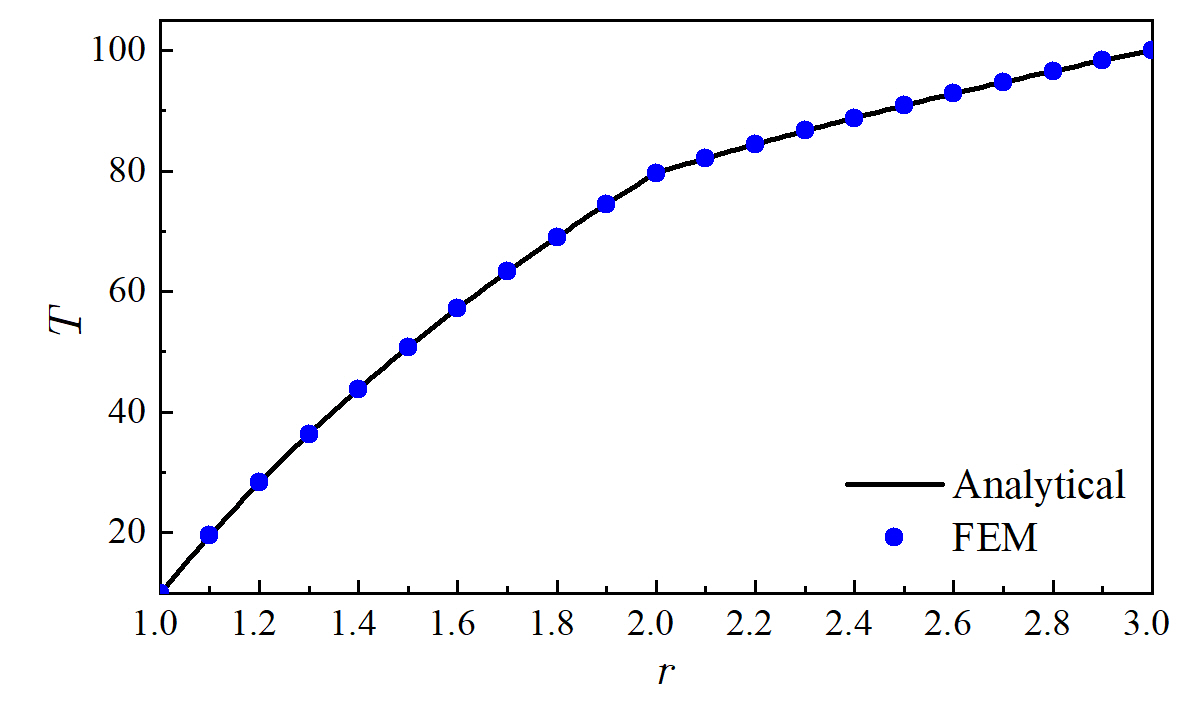
可见解析解和有限元结果是一致的。该解析解可用于验证传热方面数值模拟算法代码的准确性，特别是含界面的热传导问题。