流体体积法(VOF)求解体积分数输运方程的步骤 北京理工大学 | 李明健
流体体积法 (Volume of Fluid,VOF)是一种采用欧拉方式捕捉多相流动中相界面的数值方法,最早由 Hirt 和 Nichols 于1981年提出。在两相流问题中,VOF 方法通过定义一个 体积分数 (Volume Fraction) α 表示每个单元中目标流体(如水)所占的体积比例, α = 1 表示该单元完全为目标流体(如水)占据, α = 0 表示该单元完全被另一种流体(如空气)占据, 0 < α < 1 表示该单元包含两种流体的界面(如气-水界面)。
VOF 方法中,关键的方程是 体积分数输运方程 :
其中 u 为流体的速度矢量,该方程为对流方程。在每个时间步内,求解该方程通常包括以下步骤。
1. 获得速度场 求解 Navier-Stokes 方程,得到速度场 u ,用于后续体积分数的输运,速度场储存在单元面心上。
2. 计算法向量 采用以下公式计算法向量:
其中 m 是未进行归一化的法向量,归一化后用 n 来表示。可以看到法向量是通过体积分数的梯度计算得到的,最简单的方式是用二阶中心差分法计算梯度,但实测效果较差,处理复杂界面时法向量方向不准确,导致后续体积分数输运计算误差较大,采用四阶差分同样难以解决,二阶差分和四阶差分仅采用单元的 von Neumann 邻居,更好的方法是采用 Youngs 方法或其他混合方法,充分利用单元的 Moore 邻居数据。
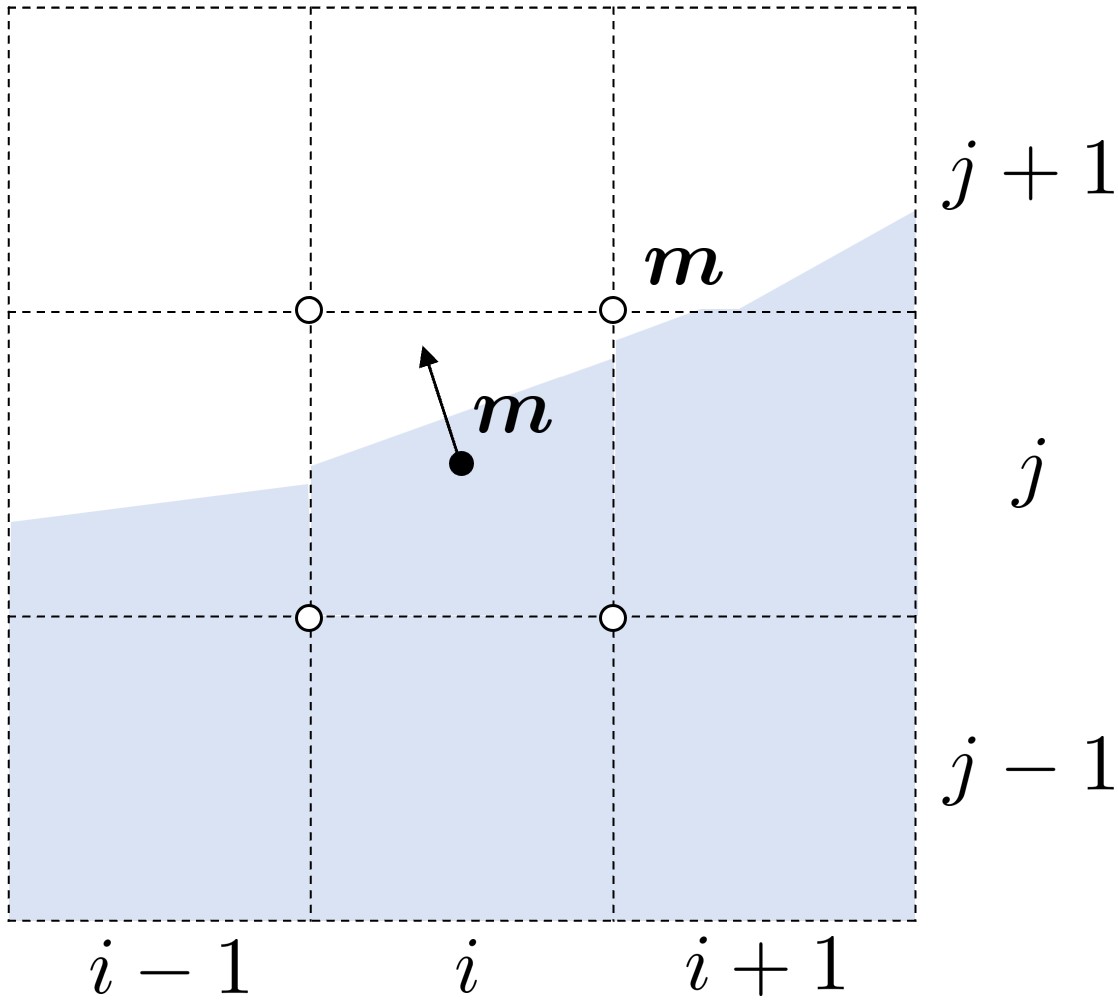
Youngs 方法中,需要根据体心的体积分数计算体心的法向量,首先,格心法向量通过节点上的中间变量平均得到:
(3) m i , j , k = 1 8 ( m i + 1 / 2 , j − 1 / 2 , k − 1 / 2 + m i − 1 / 2 , j − 1 / 2 , k − 1 / 2 + m i − 1 / 2 , j + 1 / 2 , k − 1 / 2 + m i + 1 / 2 , j + 1 / 2 , k − 1 / 2 + m i + 1 / 2 , j − 1 / 2 , k + 1 / 2 + m i − 1 / 2 , j − 1 / 2 , k + 1 / 2 + m i − 1 / 2 , j + 1 / 2 , k + 1 / 2 + m i + 1 / 2 , j + 1 / 2 , k + 1 / 2 )
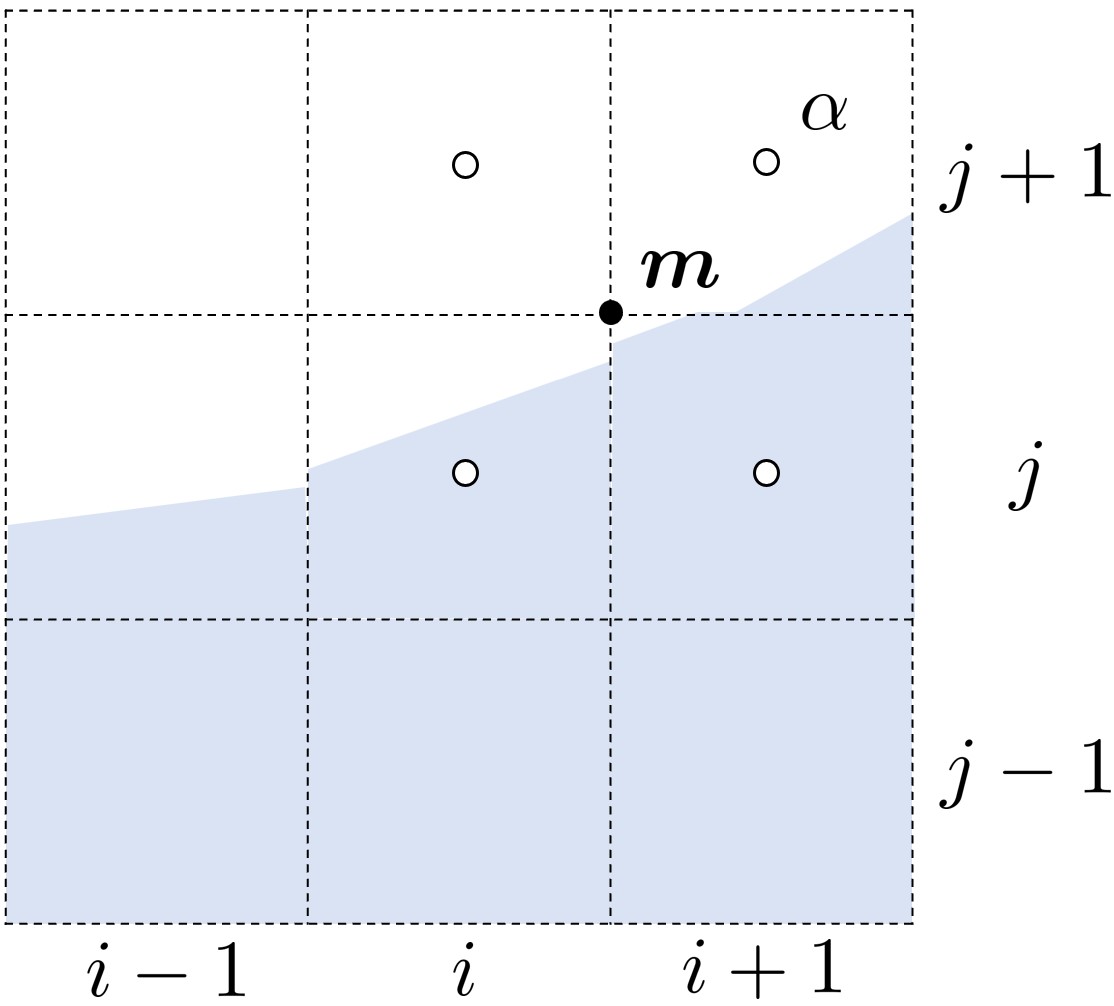
图中白点表示当前已知变量,黑点表示待求变量。法向量中间变量是通过格心的体积分数,用中心差分得到的:
(4) m x , i + 1 / 2 , j + 1 / 2 , k + 1 / 2 = − 1 4 Δ x ( α i + 1 , j + 1 , k − 1 − α i , j + 1 , k − 1 + α i + 1 , j , k − 1 − α i , j , k − 1 + α i + 1 , j + 1 , k + 1 − α i , j + 1 , k + 1 + α i + 1 , j , k + 1 − α i , j , k + 1 )
其他方向分量同理,这样为了计算格心的法向量,就需要用到 27 个模板点的体积分数。也可以采用中心列方法或其他混合方法求解法向量。
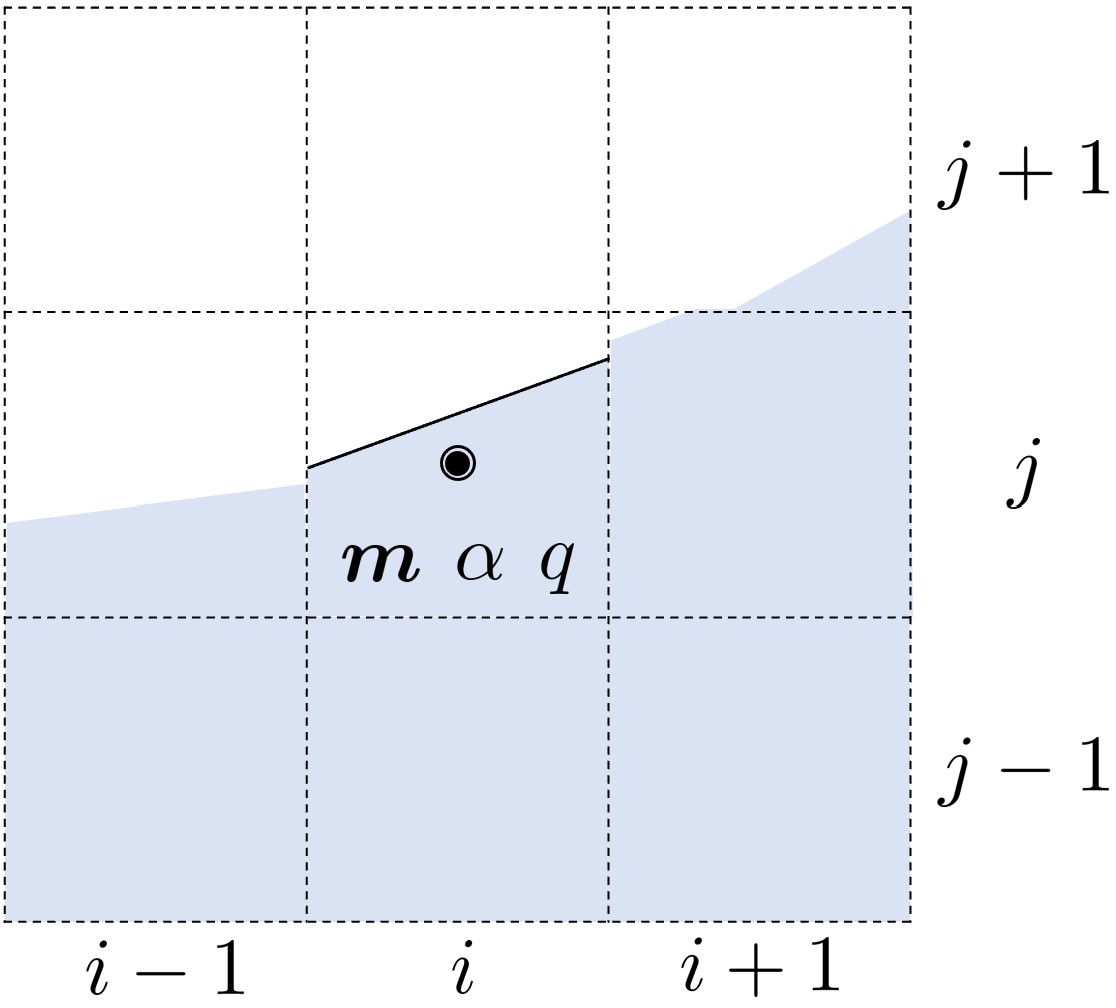
3. 界面重构 采用 PLIC(Piecewise Linear Interface Calculation) 方法,在每个含界面单元内,确定以下界面平面方程中的截距:
已知法向量 m 和体积分数 α ,目标是找到截距 q ,使得平面切割单元后,所包含的目标流体体积等于 α V cell ,其中 V cell 是单元体积 。
当单元是长方体时,可采用解析式求得 q ,当单元不是标准长方体时,可以使用牛顿迭代法等方式迭代求解得到 q 。
4. 计算通量 根据已知的面心速度场 u ,计算在时间步长 Δ t 内,通过单元各个面的流体体积通量。
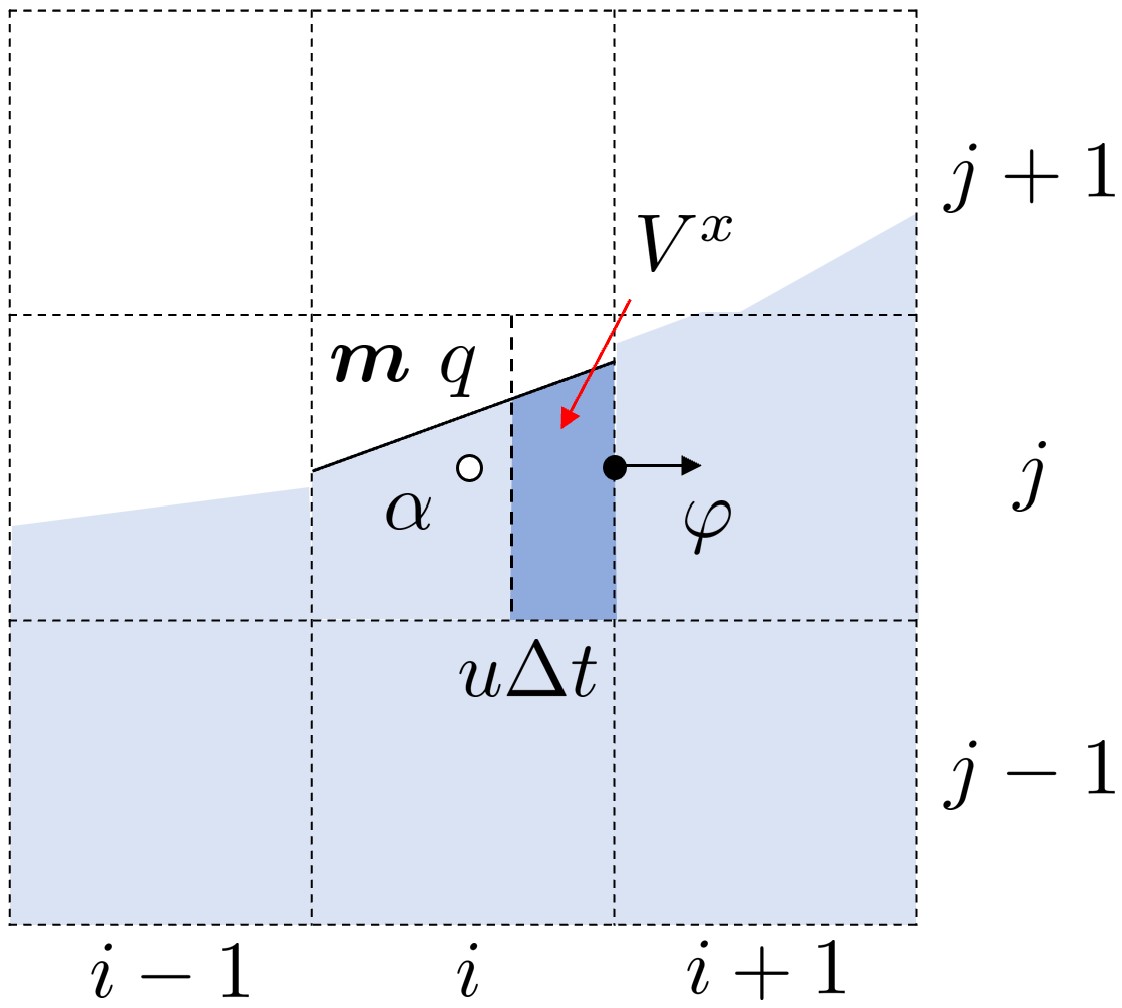
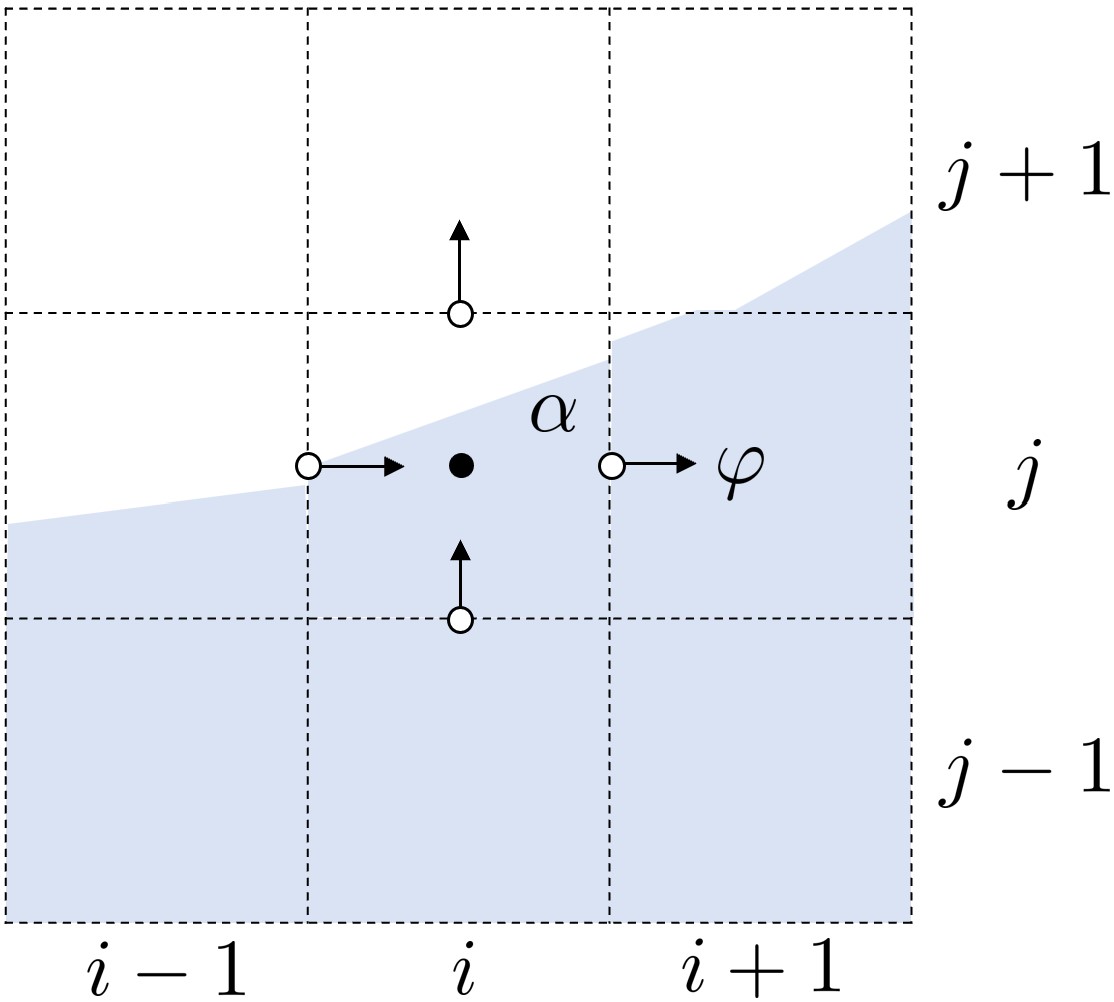
以图中 x 方向通量为例,当 u (速度水平分量)在该面上向 x 正方向流出时,其面心上的通量需要根据上游单元确定。
假设在速度驱动下,时间步 Δ t 内上游单元被界面分割的目标流体穿过该面的体积为 V x ,即下图中深色部分的体积,则该面上的通量为:
(6) φ i + 1 / 2 , j , k = V i , j , k x V cell , if u i + 1 / 2 , j , k > 0 当速度为负时,通量根据下游单元确定,这其实是一种迎风格式。
同样地,当单元是长方体时,可采用解析式求得通量,当单元不是标准长方体时,可以使用牛顿迭代法等方式迭代求解。
5. 更新体积分数 在有限体积法中,根据奥-高公式,将体积分变成面积分,对流项表示如下:
(7) 1 V ∫ V ∇ ⋅ ( α u ) d V = 1 V ∮ A ( α u ) ⋅ n d A 这样就把对流项转化成了面上通量求和的方式,而面上的通量则通过以上贡献单元的方式计算。因此,单元体积分数的增量即为其各个面输出的通量之和,表示如下:
(8) α i , j , k n + 1 = α i , j , k n + φ i − 1 / 2 , j , k − φ i + 1 / 2 , j , k + φ i , j − 1 / 2 , k − φ i , j + 1 / 2 , k + φ i , j , k − 1 / 2 − φ i , j , k + 1 / 2
该方法考虑了流入、流出的物质总和,保证了体积输运过程中的体积守恒。如果为了获得更高精度,则需要考虑三个方向输运的交叠部分,采用拉格朗日回溯等方式,用多面体求交的方式计算输运的通量。
 流体体积法(VOF)求解体积分数输运方程的步骤
流体体积法(VOF)求解体积分数输运方程的步骤