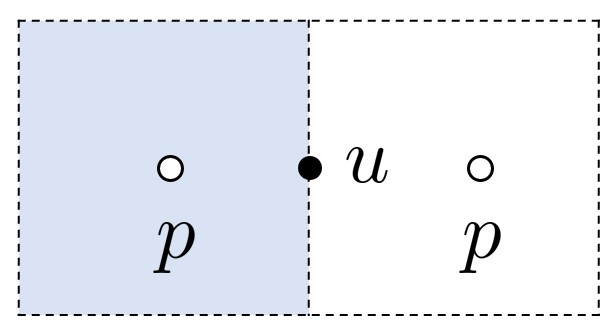流体体积法(VOF)求解两相流问题的步骤
流体体积法(VOF)求解两相流问题的步骤
北京理工大学 | 李明健
控制方程:
对于两相流动,采用 one-fluid 模型,即用统一的物理场描述两种流体,用体积分数的方式区分。例如,密度场可表示为如下形式:
其中 为体积分数, 和 分别为两种流体的密度。对于粘度等其他物理量,用同样的方式处理。
连续性方程
不可压流体问题的连续性方程通常写为速度无散形式如下:
动量方程
Navier-Stokes方程采用守恒形式如下:
式中,,,, 分别为速度、密度、压力、粘度、体力。
求解方法:
采用 Chorin 投影法,我们把N-S方程分裂成以下形式:
其中 和 分别为对流项和扩散项,两式相加即为N-S方程。
对第二式取散度得到压力泊松方程:
采用交错网格,在格心求解压力, 面心求解速度。
对流项
对流项具体展开形式为:
在有限体积法中,根据奥-高公式,将体积分变成面积分,对流项表示如下:
以 方向面心对流项分量为例:
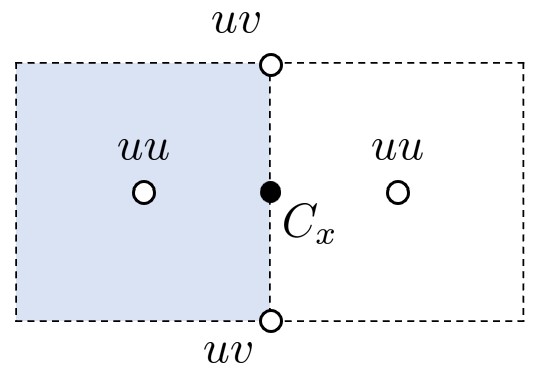
其中 表示三个方向的面积,黑色圆点表示待计算的物理量,白色圆点表示插值模板点。计算面心上的对流项,需要用到格心和棱心处被输运的速度,这些速度需要从其他面心位置插值过来,用QUICK(Quadratic upstream interpolation for convective kinematics)三阶迎风格式插值,相比普通中心差分可以达到更高的精度。以 方向格心速度 为例,插值形式如下:
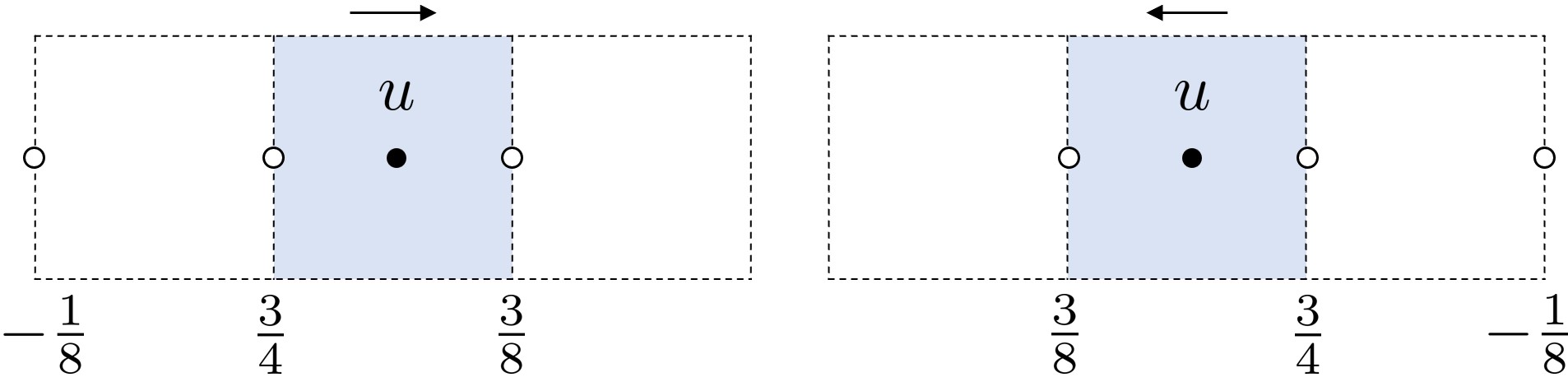
以 方向棱心速度 为例,插值形式如下:
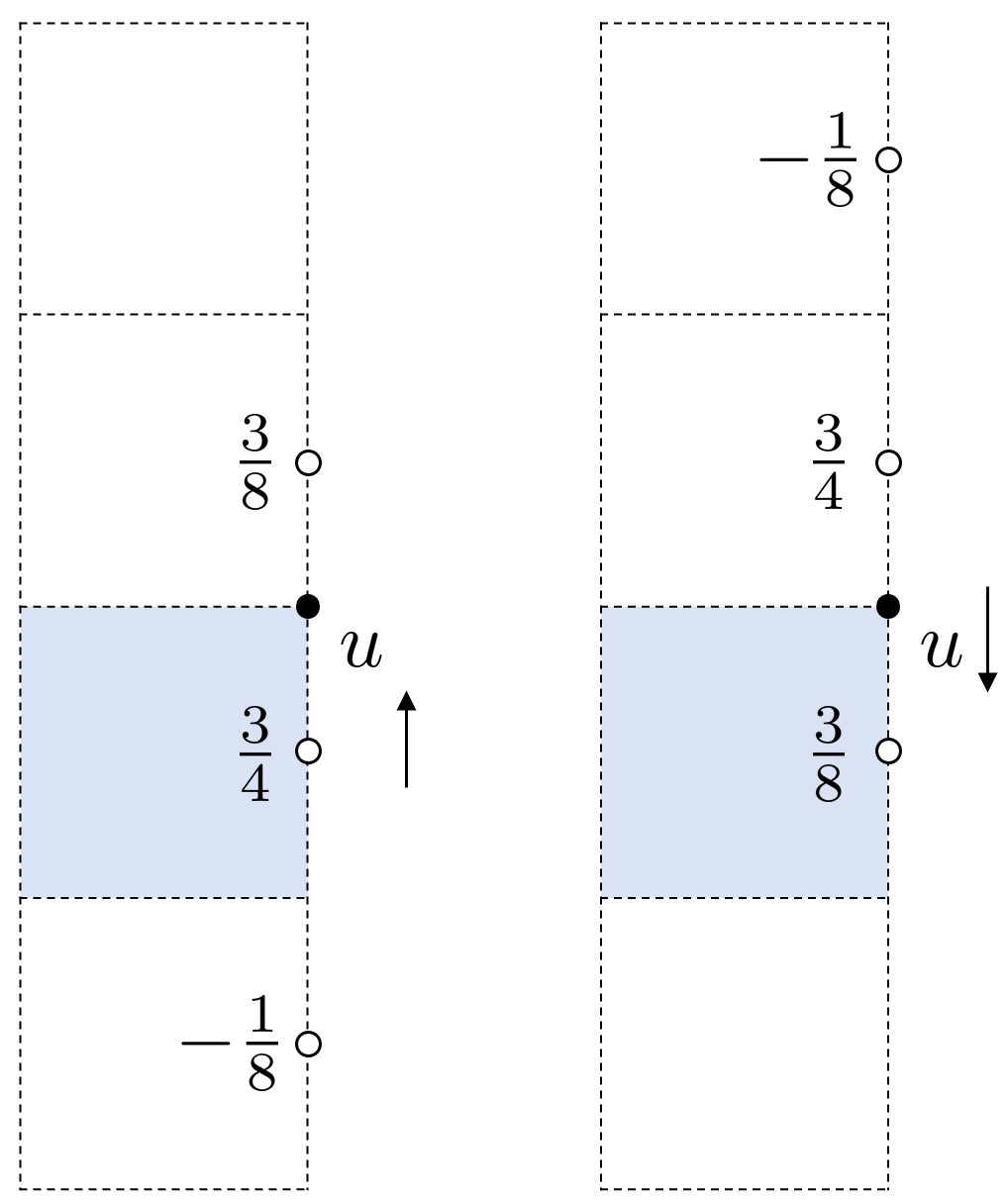
类似可以得到所有速度分量,并得到对流项所有分量。
扩散项
粘性扩散项具体展开形式为:
其中粘性应力具体展开形式为:
扩散项写成面积分的形式为:
以 方向面心分量为例:
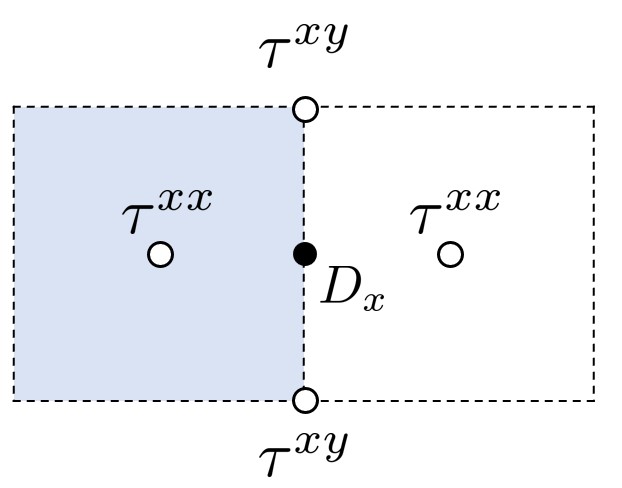
粘性应力分量采用二阶中心差分得到,以其中两个分量为例:
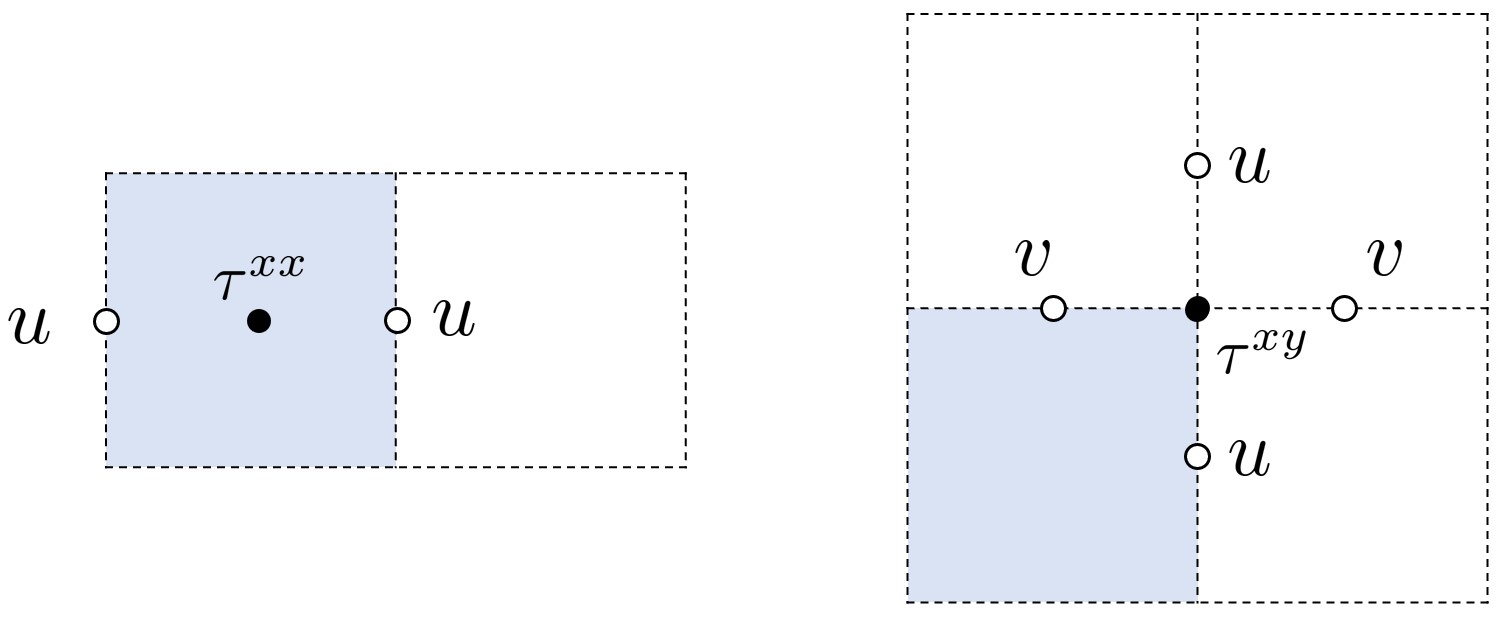
其余分量同理,最终得到扩散项所有分量。
速度预测
Chorin 投影法第一步是预测一个中间速度:
预测速度在面上求解:
压力泊松方程
Chorin 投影法第二步是求解压力泊松方程:
在格心求解格式为:
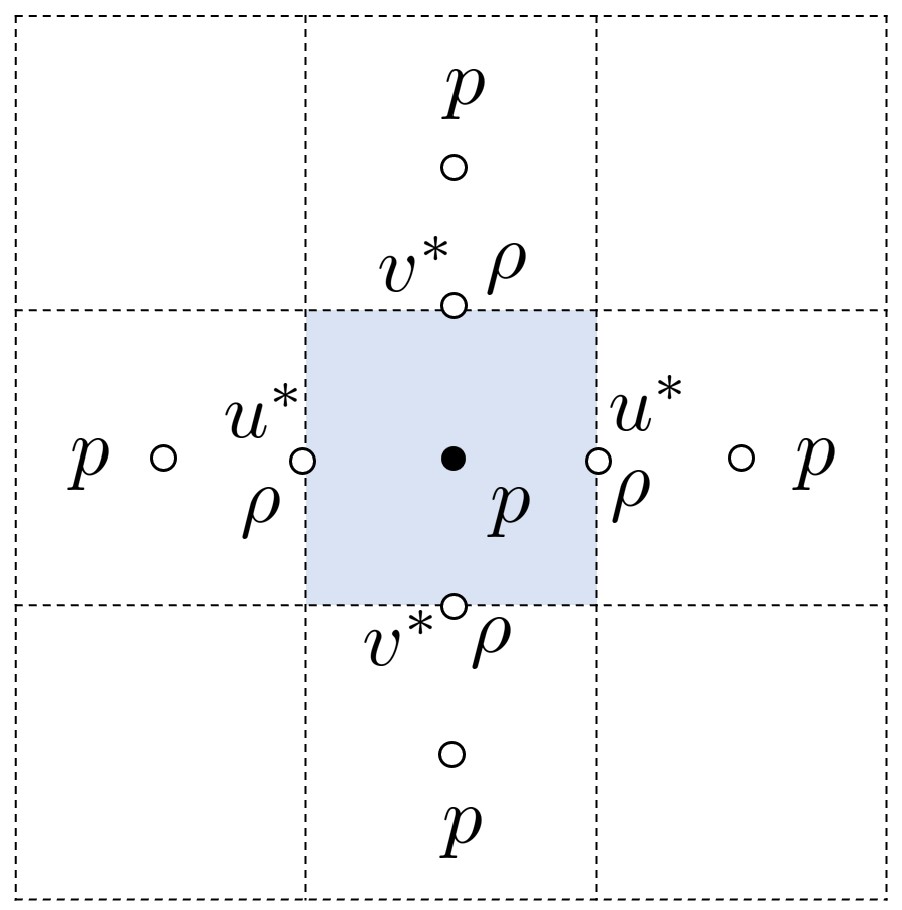
压力泊松方程可以采用SOR(successive over-relaxation)迭代法求解,或共轭梯度等其他方法。
速度修正
在面心用压力梯度修正中间速度,得到最终的速度场:
在面心求解格式为:
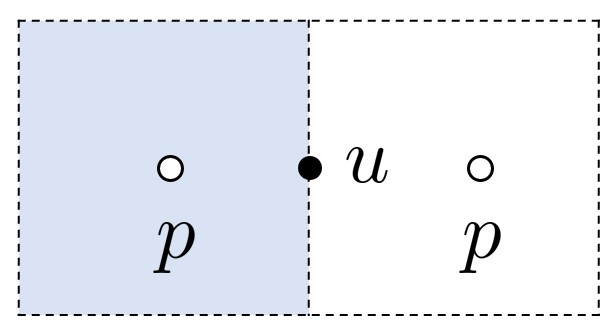
密度和粘度
面心上的密度和粘度可以用格心直接平均,也可以通过PLIC中的切割方法得到面心的体积分数,随后,在面上用体积分数更新密度和粘度:
 流体体积法(VOF)求解两相流问题的步骤
流体体积法(VOF)求解两相流问题的步骤